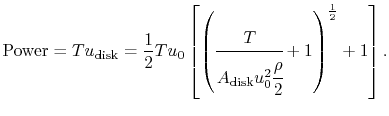I continue to claim that your procedure doesn’t make any sense. In order to get myself out of too much guessing I looked up the code.
In the multicopter code I find these three functions of relevance:
- float AP_MotorsMulticopter::apply_thrust_curve_and_volt_scaling(float thrust)
- void AP_MotorsMulticopter::update_lift_max_from_batt_voltage()
- int16_t AP_MotorsMulticopter::calc_thrust_to_pwm(float thrust_in)
The function update_lift_max_from_batt_voltage() is responsible for calculating the factors _batt_voltage_filt and _lift_max, which are used to compensate for the effects of a reducing battery voltage. For the present discussion this effect is irrelevant, and both can be set to 1.0, meaning full battery.
The math done in the other two functions can be summarized as follows, where I have simplified the variable names in an obvious manner, to make the equations better readable:
// converts thrust_in = [0…1] to throttle_ratio = [0…1]
throttle_ratio =
[ -(1.0-expo) + sqrt{ (1.0-expo)*(1.0-expo) + 4.0 * expo * lift_max * thrust_in } ]
/
[ 2.0 * expo * batt_voltage_filt ]
// converts throttle_ratio = [0…1] to X = [spin_min…spin_max]
X = spin_min + (spin_max - spin_min) * throttle_ratio(thrust_in)
// converts X = [0…1] to pwm = [pwm_min…pwm_max]
thrust_to_pwm = pwm_min + (pwm_max - pwm_min) * X
The latter equation is irrelevant to us, since it adapts to the specific ESC pwm range, which for our UAVCAN ESCs should be set to 1000,2000. Thus, we have to look at how the plot of X vs thrust_in looks like.
thrust_in is in the range of [0…1], and by virtue of how throttle_ratio is calculated, also throttle_ratio is in the range of [0…1], where moreover throttle_ratio(0) = 0 and throttle_ratio(1) = 1. So it spans the full range of values from 0 to 1. The second equation limits that to the range [spin_min…spin_max]. Thus we have a function X(thrust_in) which on the x axis goes from 0 to 1, and on the y axis from spin_min to spin_max.
What we need for fitting is the inverse function, thrust_in(X). On the x axis it therefore goes from spin_min to spin_max, and on the y axis it goes from 0 to 1. In between it is a poly, i.e.
thrust_in = (1-expo) * X_norm + expo * X_norm^2
where
X_norm = (X - spin_min) / (spin_max - spin_min)
This leads to exactly ‘my’ procedure of applying spin_min and spin_max, as well as to the fitting function I have used.
In summary, your proposed fitting strategy appears to be arbitrary in the sense that it doesn’t bear any relation to what is calculated in the code.
EDIT: I however, unfortunately, have implemented ‘my’ procedure in the script incorrectly! So, in some sense it is correct to say that I have not applied spin_min/max correctly, since I didn’t do exactly what I intended to do. The effect will be to reduce the value of expo, which is now about 0.75-0.80. However, my statement that the ‘alternative’ fitting procedure doesn’t make any sense, and is incorrect as it doesn’t reflect what the code does, remains valid. In fact, it yielded 0.59, while one should use 0.75-0.80 in order to make the calculations in ArduCopter represent the data. If that difference is considered irrelevant, then the whole concept is irrelevant, and one doesn’t need to bother with data at all.
I note that for this aspect it is irrelevant if the data, which is an estimated thrust curve, is ‘good’ or ‘bad’. The above points are based on one and the same data set.
EDIT 2: I’d like to add: Obviously the value of MOT_THST_EXPO is, for one and the same motor system, very sensitive to the choice of the MOT_SPIN_MIN/MAX parameters. This makes this quantity pretty much useless for characterizing the thrust characteristics, e.g., for comparing different drive systems. It’s a said before, one fits an elephant here. So, a better quantity needs to be found. I think that’s an important result, at least it is to me it, since I actually was kind of believing that MOT_THST_EXPO would be something like a characteristic exponent, which it is not. Thrust curves (thrust cs rpm) are usually described by an algebraic function, i.e., ‘real’ exponents. I guess it would be interesting to see if that approach could give a better characteristic also for the thrust vs pwm curves.
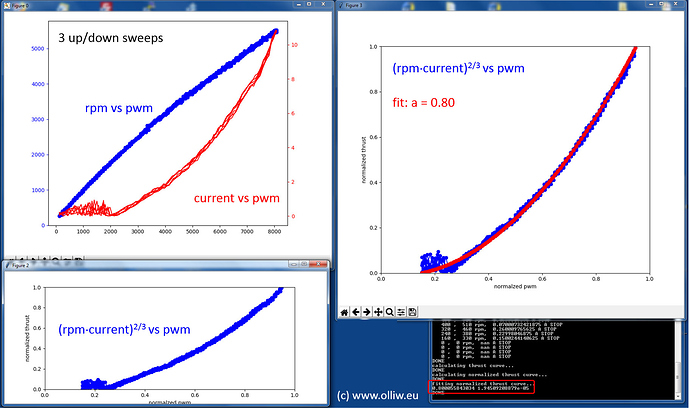
The current measurement however, as I’ve pointed out earlier, indeed doesn’t look reliable here; I’ve brought this already to Felix’s attention.
